Engine & Intake FAQ's
#1
Administrator

Thread Starter
Introduction
Valve performance plays a significant role in the overall power production of an engine. If the valves are too small, the air flow will be restricted, and the engine torque will decrease. The airflow through the inlet and the exhaust ports of an engine is unsteady, due to the periodic opening and closing of the inlet and the exhaust valves.
There are several types of valves that are used: a poppet, rotary, disc and a sleeve. The most common valve is the poppet valve. The poppet valve is inexpensive and has good sealing properties, making it such a popular choice. The following evaluation will assume poppet valves are used for both the inlet and exhaust ports.
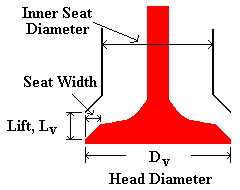
Figure 1. Schematic of the Valve and Valve Port
Generally the inlet port is circular, and about 44-48% of the size of the cylinder bore, no larger than needed to produce the desired power.
Another geometric parameter of a valve is the lift. When the value is just above the seat, it is considered to be low lift. At low lift the inlet flow remains attached to the valve seat, taking the form of a wall jet. At intermediate lift, the flow begins to separate from the valve head at the inner edge of the valve seat. Finally at high lift, the flow separates from the inner edge of the valve seat as well, taking the form of a free jet.
The following two applets shows the behavior of the flow as the value opens.
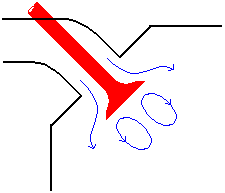
Due to the constant opening and closing of the valves, the cross sectional area through which the flow passes through changes. This area is referred to as the effective area. This area is defined as:
Ae = Ac (q ) Cd(q)
Where:
Ac = curtain area
Cd = discharge coefficient
The curtain area, Ac, can be defined in several ways. A simple definition of the curtain area is given by:
Ac = 3.14159*Dv Lv
Where:
Dv = diameter of the valve
Lv = lift
The lift and the discharge coefficient both vary with the crank angle. The discharge coefficient is determined experimentally. This coefficient accounts for the real gas flow effects. The discharge coefficient decreases slightly with lift since the jet fills less of the reference curtain area as it transforms from an attached jet to a separated free jet. A representative value of the discharge coefficient is Cd = 0.6.
The lift and Cd are determined from experiment. If the lift and Cd profiles are known , the effective area can be found as a function of the crank angle.
Exhaust Flow
The exhaust process is broken up into two parts: the exhaust blowdown and the exhaust stroke. The exhaust blowdown is modeled as a constant volume process, and the exhaust stroke is modeled as a constant pressure process. When the exhaust valve opens, the cylinder pressure is usually high enough so that sonic flow occurs at the valve and blowdown is very rapid.
Valve Timing
The opening and closing of the exhaust and inlet valve overlap each other. The following figure shows the overlapping of the two valves.
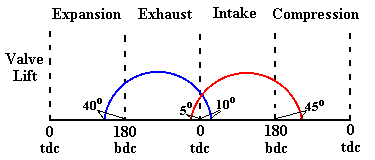
Figure 3. Intake and Exhaust Valve Timing
The inlet valve begins to open before top dead center so that there will be a large effective area, Ae, at the start of induction. The exhaust valve begins to open before bottom dead center to give the combustion products time to escape
The speed of the engine determines how early the exhaust valve opens. At low RPM's the valve opens early and at high RPM's the valve opens late.
Intake and Exhaust Tuning
By proper choice of the length of the intake and exhaust piping, the performance of internal combustion engines can be increased. Inlet and exhaust valve opening and closing creates a compressible flow process in which pressure waves flow back and forth through the inlet and exhaust system. The appropriate pipe length can be estimated through solution of the compressible flow equations. Alternatively, a number of heuristic pipe length equations have been developed.
A pressure wave is created when an intake or exhaust valve is opened. The wave propagates through the the fluid in the pipe at the speed of sound c. When this wave encounters a change in cross sectional area, such as the end of the pipe, a wave of opposite sign will be reflected from the end of the pipe. Based on the time it takes for this wave to return back to the valve, the length of the pipe can be determined.
Intake Valve
For example,when the inlet valve opens, a rarefaction wave is sent upstream from the valve. When this wave encounters a change in area such as the intake manifold, a compression wave is generated and sent downstream back to the inlet valve. This compression wave increases the local density of the inlet flow, a process called the "ram effect".
Experimentally, it has been found that a significant gain in volumetric efficiency is attained when the reflected compression wave returns when the piston is at a crank angle of 90o. At this point the piston velocity is maximum. Matching the time it takes for the wave to return with the characteristic piston time, the required length of the pipe can be found.
The velocity of the wave is given by:
velocity = distance / time
The distance is twice the pipe length, 2L. The time is found from the engine speed.
Solving for the pipe length, L, results in:
The term c is the speed of sound. It is dependent on the temperature T (in degrees Kelvin) of the incoming flow, the air ideal gas constant R, and the specific heat ratio k. The speed of sound is given by the following equation:
Exhaust Valve
When the exhaust valve opens, a compression wave is sent downstream and reflects back as a rarefaction wave when an opening in the exhaust system is encountered. Experimentally it has been found that the optimum position of the piston when the wave returns is 120o. At this position the remaining exhaust gas can be scavenged from the combustion chamber. The required length of the exhaust pipe can then be determined.
Vehicle Power Requirements
How much power does it take to go 60 mph? 80 mph? The weight of the car and its speed all are factors that affect the amount of power required. The force balance of a vehicle is shown in Figure 4.
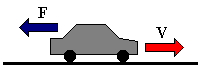
The forces acting on the car are caused by internal, tire, and air resistance. The resultant of these forces, the total drag force, FD, can be estimated by the following equation:
Where:
cR = coefficient of rolling resistance
cD = drag coefficient
m = mass of vehicle [kg]
A = frontal surface area [m2]
g = 9.8 m/s
r = density of are, 1.2 kg/m3 @STP
The coefficients of rolling resistance and drag are determined from experiment. A typical value for the coefficient of rolling resistance is 0.015. The drag coefficient for cars varies, a value of 0.3 is commonly used.
The power output requirement can be determined from the drag force given above and the vehicle velocity.
P = FDV
The basic definition for the acceleration force (neglecting drag !) is given by:
F = ma
Assuming that the force required to accelerate a vehicle from 0 to 60 mph can be determined from the above equation, then the power necessary to accelerate to a given velocity is:
P = maV
Where:
m = mass of the vehicle
a = acceleration = DV/DT
DV = 60 - 0 = 60 mph = 26.82 m/s
V = final velocity, 60 mph
intake effective area applet http://www.engr.colostate.edu/~allan/fluid...ea/effarea.html
pipe length applet http://www.engr.colostate.edu/~allan/fluid...ength/pipe.html
vehicle power applet http://www.engr.colostate.edu/~allan/fluid...ower/power.html
vehicle acceleration applet http://www.engr.colostate.edu/~allan/fluid...accelerate.html
Valve performance plays a significant role in the overall power production of an engine. If the valves are too small, the air flow will be restricted, and the engine torque will decrease. The airflow through the inlet and the exhaust ports of an engine is unsteady, due to the periodic opening and closing of the inlet and the exhaust valves.
There are several types of valves that are used: a poppet, rotary, disc and a sleeve. The most common valve is the poppet valve. The poppet valve is inexpensive and has good sealing properties, making it such a popular choice. The following evaluation will assume poppet valves are used for both the inlet and exhaust ports.

Figure 1. Schematic of the Valve and Valve Port
Generally the inlet port is circular, and about 44-48% of the size of the cylinder bore, no larger than needed to produce the desired power.
Another geometric parameter of a valve is the lift. When the value is just above the seat, it is considered to be low lift. At low lift the inlet flow remains attached to the valve seat, taking the form of a wall jet. At intermediate lift, the flow begins to separate from the valve head at the inner edge of the valve seat. Finally at high lift, the flow separates from the inner edge of the valve seat as well, taking the form of a free jet.
The following two applets shows the behavior of the flow as the value opens.

Due to the constant opening and closing of the valves, the cross sectional area through which the flow passes through changes. This area is referred to as the effective area. This area is defined as:
Ae = Ac (q ) Cd(q)
Where:
Ac = curtain area
Cd = discharge coefficient
The curtain area, Ac, can be defined in several ways. A simple definition of the curtain area is given by:
Ac = 3.14159*Dv Lv
Where:
Dv = diameter of the valve
Lv = lift
The lift and the discharge coefficient both vary with the crank angle. The discharge coefficient is determined experimentally. This coefficient accounts for the real gas flow effects. The discharge coefficient decreases slightly with lift since the jet fills less of the reference curtain area as it transforms from an attached jet to a separated free jet. A representative value of the discharge coefficient is Cd = 0.6.
The lift and Cd are determined from experiment. If the lift and Cd profiles are known , the effective area can be found as a function of the crank angle.
Exhaust Flow
The exhaust process is broken up into two parts: the exhaust blowdown and the exhaust stroke. The exhaust blowdown is modeled as a constant volume process, and the exhaust stroke is modeled as a constant pressure process. When the exhaust valve opens, the cylinder pressure is usually high enough so that sonic flow occurs at the valve and blowdown is very rapid.
Valve Timing
The opening and closing of the exhaust and inlet valve overlap each other. The following figure shows the overlapping of the two valves.

Figure 3. Intake and Exhaust Valve Timing
The inlet valve begins to open before top dead center so that there will be a large effective area, Ae, at the start of induction. The exhaust valve begins to open before bottom dead center to give the combustion products time to escape
The speed of the engine determines how early the exhaust valve opens. At low RPM's the valve opens early and at high RPM's the valve opens late.
Intake and Exhaust Tuning
By proper choice of the length of the intake and exhaust piping, the performance of internal combustion engines can be increased. Inlet and exhaust valve opening and closing creates a compressible flow process in which pressure waves flow back and forth through the inlet and exhaust system. The appropriate pipe length can be estimated through solution of the compressible flow equations. Alternatively, a number of heuristic pipe length equations have been developed.
A pressure wave is created when an intake or exhaust valve is opened. The wave propagates through the the fluid in the pipe at the speed of sound c. When this wave encounters a change in cross sectional area, such as the end of the pipe, a wave of opposite sign will be reflected from the end of the pipe. Based on the time it takes for this wave to return back to the valve, the length of the pipe can be determined.
Intake Valve
For example,when the inlet valve opens, a rarefaction wave is sent upstream from the valve. When this wave encounters a change in area such as the intake manifold, a compression wave is generated and sent downstream back to the inlet valve. This compression wave increases the local density of the inlet flow, a process called the "ram effect".
Experimentally, it has been found that a significant gain in volumetric efficiency is attained when the reflected compression wave returns when the piston is at a crank angle of 90o. At this point the piston velocity is maximum. Matching the time it takes for the wave to return with the characteristic piston time, the required length of the pipe can be found.
The velocity of the wave is given by:
velocity = distance / time
The distance is twice the pipe length, 2L. The time is found from the engine speed.
Solving for the pipe length, L, results in:
The term c is the speed of sound. It is dependent on the temperature T (in degrees Kelvin) of the incoming flow, the air ideal gas constant R, and the specific heat ratio k. The speed of sound is given by the following equation:
Exhaust Valve
When the exhaust valve opens, a compression wave is sent downstream and reflects back as a rarefaction wave when an opening in the exhaust system is encountered. Experimentally it has been found that the optimum position of the piston when the wave returns is 120o. At this position the remaining exhaust gas can be scavenged from the combustion chamber. The required length of the exhaust pipe can then be determined.
Vehicle Power Requirements
How much power does it take to go 60 mph? 80 mph? The weight of the car and its speed all are factors that affect the amount of power required. The force balance of a vehicle is shown in Figure 4.

The forces acting on the car are caused by internal, tire, and air resistance. The resultant of these forces, the total drag force, FD, can be estimated by the following equation:
Where:
cR = coefficient of rolling resistance
cD = drag coefficient
m = mass of vehicle [kg]
A = frontal surface area [m2]
g = 9.8 m/s
r = density of are, 1.2 kg/m3 @STP
The coefficients of rolling resistance and drag are determined from experiment. A typical value for the coefficient of rolling resistance is 0.015. The drag coefficient for cars varies, a value of 0.3 is commonly used.
The power output requirement can be determined from the drag force given above and the vehicle velocity.
P = FDV
The basic definition for the acceleration force (neglecting drag !) is given by:
F = ma
Assuming that the force required to accelerate a vehicle from 0 to 60 mph can be determined from the above equation, then the power necessary to accelerate to a given velocity is:
P = maV
Where:
m = mass of the vehicle
a = acceleration = DV/DT
DV = 60 - 0 = 60 mph = 26.82 m/s
V = final velocity, 60 mph
intake effective area applet http://www.engr.colostate.edu/~allan/fluid...ea/effarea.html
pipe length applet http://www.engr.colostate.edu/~allan/fluid...ength/pipe.html
vehicle power applet http://www.engr.colostate.edu/~allan/fluid...ower/power.html
vehicle acceleration applet http://www.engr.colostate.edu/~allan/fluid...accelerate.html

